Creating a village-level shapefile for Pakistan using a Voronoi Tessellation

-
Using the latitude and longitude coordinates of human settlements in Pakistan, i create polygons that approximate the shape of villages. 

 I recently found a shapefile hosted on the UN's Humanitarian Data Exchange (HUMDATA) portal which contains the coordinates of villages in Pakistan: 


 Village level shapefiles are extremely hard to come by, and most countries don't publicly release data at such a fine level of spatial disaggregation. However, conducting analysis at this level can drastically augment statistical power by increasing the number of observations. Consider the relative quantities of various administrative units in Pakistan:
Districts are probably the most common sub-national administrative units of analysis in econometrics. In Pakistan, Tehsil and (sometimes) Union Council level data and shapefiles are available, allowing one to go below the district level. Even so, there are 46 times more villages than Union Councils and 1,696 more villages than Districts. If one were to conduct a 10 period panel regression using districts, we would have n=1,540. If the same regression were conducted with villages, we would have n=2,612,170. 

 As remarkable as finding such a file is, the structure of the data is rather unhelpful: villages are identified as one-dimensional points. This disables many of the most useful properties of having administrative boundary shapefiles. Imagine trying to do any analysis with a shapefile of U.S. States, but instead of having polygons denoting state boundaries, you just had the population centers: 



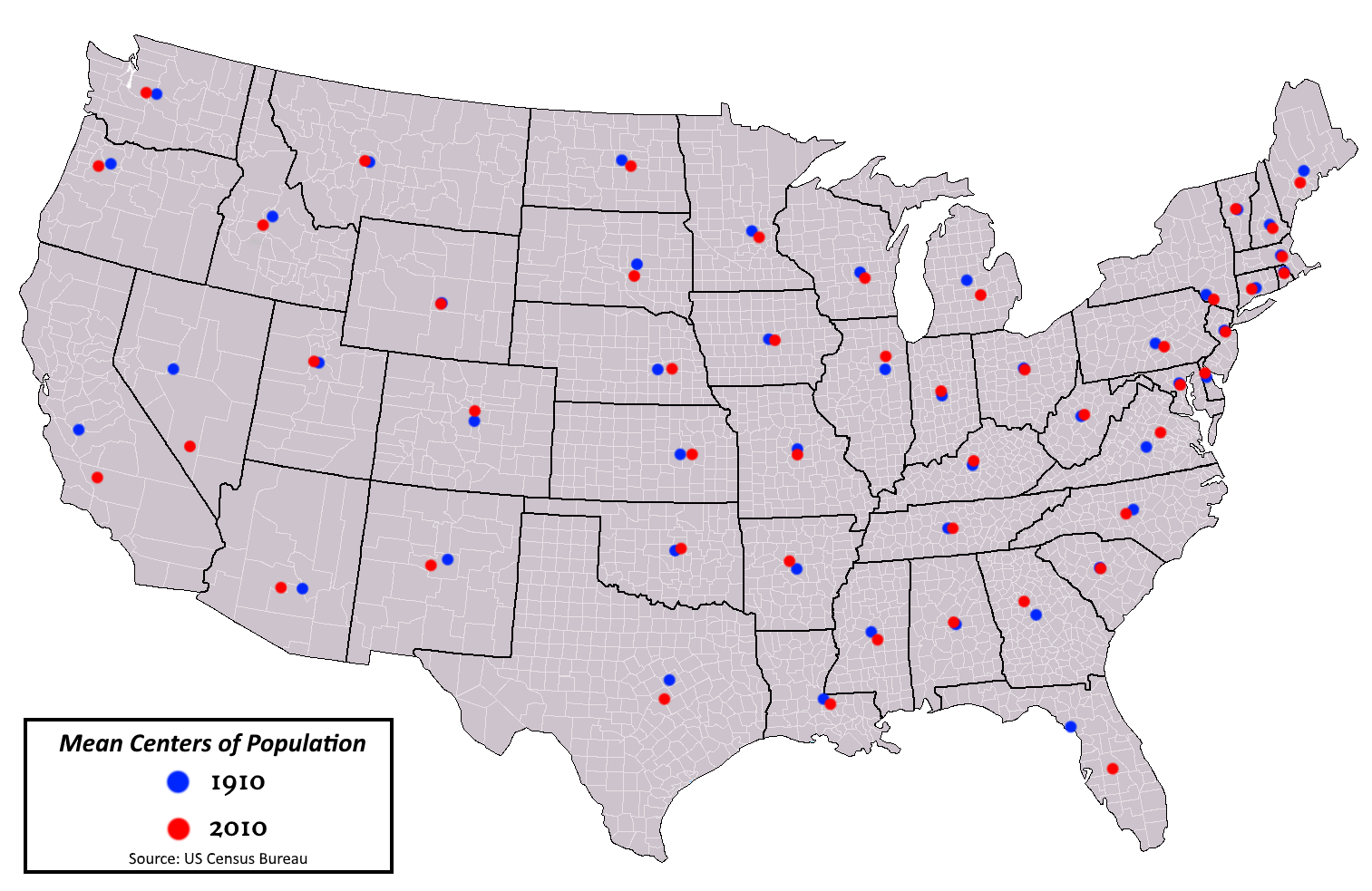
 Suppose you wanted to know what percent of a state was covered in cropland versus forest (i.e., calculate zonal statistics), or suppose you had the coordinates of every walmart in the U.S., and wanted to count how many were in each state (i.e., perform a spatial join). Though this problem is less severe with village-level points as they are much closer together, the overall problem remains. 

 Thus, to make this shapefile more useful, we must turn points into polygons. The most intuitive way of doing so is to generate a Voronoi tessellation; this creates polygons  from input coordinates such that any point within a polygon is closer to its input coordinate than any other:


If you're interested in the specifics of how a Voronoi tessellation works, Nico Belmonte has a great blog post on the subject.

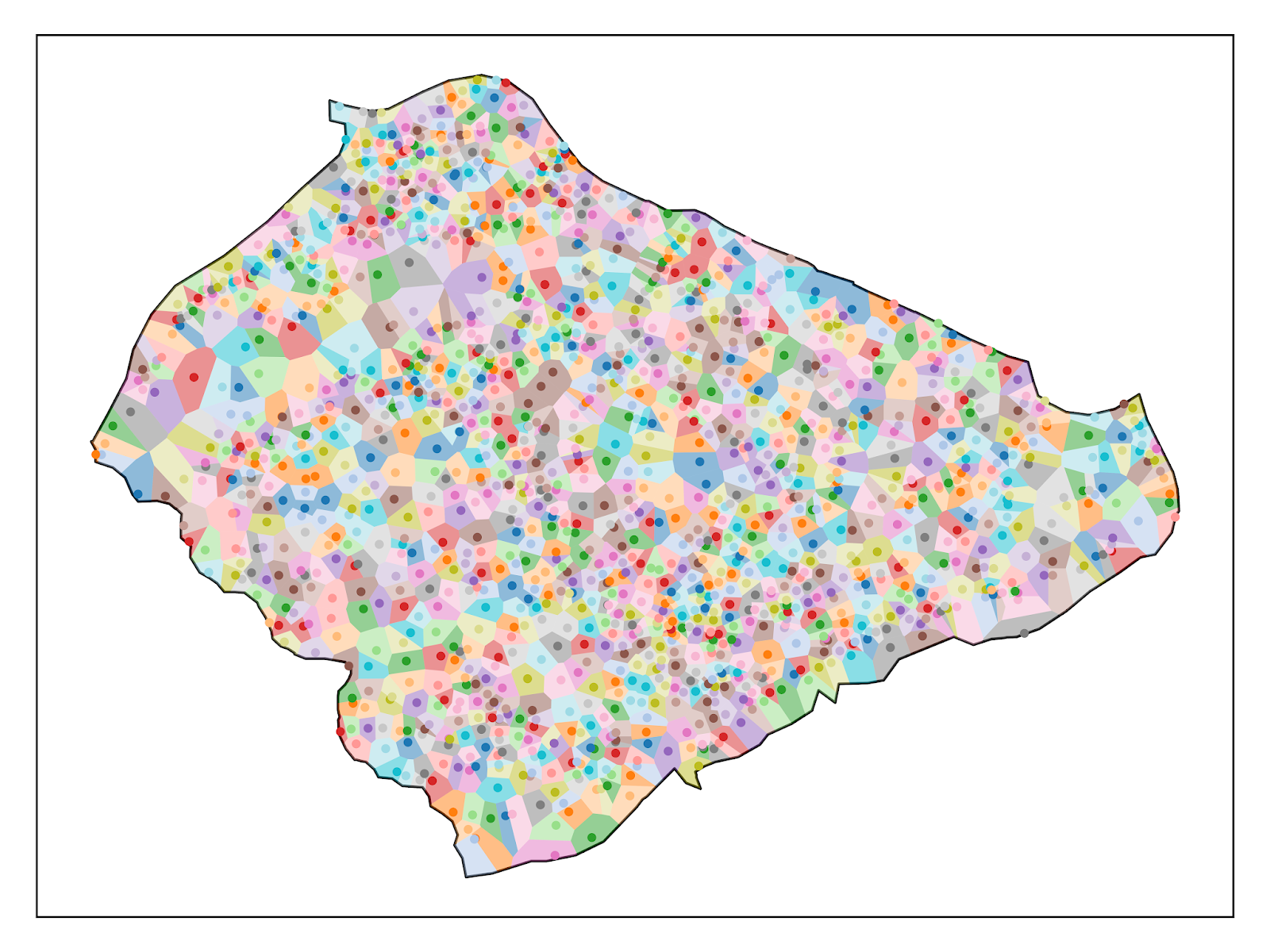
Using the geovoronoi and geopandas packages in Python it was simple enough to create a voronoi polygons from the points in the original shapefile. Consider the example of Gujrat:
These shapefiles and images were generated using the code below:

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
import logging

import matplotlib.pyplot as plt
import numpy as np
import geopandas as gpd
import pandas as pd
from geovoronoi import coords_to_points, points_to_coords, voronoi_regions_from_coords
from geovoronoi.plotting import subplot_for_map, plot_voronoi_polys_with_points_in_area
import os
from matplotlib.pyplot import figure
from fuzzywuzzy import fuzz
from fuzzywuzzy import process
from fuzzywuzzy.fuzz import ratio
import multiprocessing
import shutil 

plt.switch_backend('agg')
logging.basicConfig(level=logging.INFO)
geovoronoi_log = logging.getLogger('geovoronoi')
geovoronoi_log.setLevel(logging.INFO)
geovoronoi_log.propagate = True

arcdir="/data/eg-cluster-dir/eg-username/"
regdir="/Users/ollie/PakistanPoints/"

arc=True
if arc:
 dbf=arcdir+"/Pakistan Village Shapefile/PAK_Settlements_NGA_2017_20181122.dbf"
 shp=arcdir+"Admin Boundaries/District_Boundary.shp"
 pakistan_voronois = arcdir+"Pakistan Voronoi/"
else:
 dbf=regdir+"Pakistan Village Shapefile/PAK_Settlements_NGA_2017_20181122.dbf"
 shp=regdir+"Admin Boundaries/District_Boundary.shp"
 pakistan_voronois = regdir+"/Pakistan Voronoi/"

village=gpd.read_file(dbf)

village=village[village['PROVINCE']=="Punjab"]
village.DISTRICT=village.DISTRICT.str.upper()

areas=gpd.read_file(shp)
areas=areas[areas['PROVINCE']=='PUNJAB']
districts=[]
for i in areas.DISTRICT:
 districts.append(i)

threading=True

if threading:

 def doVoronoiForDistrict(districtNumber):
  i=districts[districtNumber-1]

  if i=="MUZAFARGARH":
   ii='MUZAFFARGARH'
  if i=="D G KHAN":
   ii='DERA GHAZI KHAN'
  if i=="T. T SINGH":
   ii='TOBA TEK SINGH'
  if i=="R Y KHAN":
   ii='RAHIM YAR KHAN'

  villages=village[village['DISTRICT']==i]
  if len(villages)==0:
   villages=village[village['DISTRICT']==ii]

  villages.reset_index(inplace=True)
  villages=villages.iloc[:10]
  coords = np.vstack((villages.LONG, villages.LAT)).T

  district=str(i)
  dist_dir=pakistan_voronois+district
  try:
   os.mkdir(dist_dir)
  except:
   shutil.rmtree(dist_dir, ignore_errors=True)
   os.mkdir(dist_dir)

  area=areas[areas['DISTRICT']==i]
  print('CRS:', area.crs)   # gives epsg:4326 -> WGS 84

  area_shape = area.iloc[0].geometry   # get the Polygon


  # use only the points inside the geographic area
  pts = [p for p in coords_to_points(coords) if p.within(area_shape)]  # converts to shapely Point


  coords = points_to_coords(pts)   # convert back to simple NumPy coordinate array
  #del pts

  #
  # calculate the Voronoi regions, cut them with the geographic area shape and assign the points to them
  #

  poly_shapes, pts, poly_to_pt_assignments = voronoi_regions_from_coords(coords, area_shape)
  villages.drop(columns={'geometry'}, inplace=True)
  villages['geometry'] = None


  count=-1
  #quit()
  for i in poly_to_pt_assignments:
   count=count+1
   try:
    for f in i:
     villages.loc[[f],'geometry']=poly_shapes[count]
     #print("polygon:",count,"point:", f)
   except:
    #print("skipped", "polygon:",count,"point:", f)
    pass

  villages.to_file(dist_dir+"/"+district+".dbf")
  fig, ax = subplot_for_map()
  plot_voronoi_polys_with_points_in_area(ax, area_shape, poly_shapes, coords, poly_to_pt_assignments)
  #plot_voronoi_polys_with_points_in_area(ax, area_shape, poly_shapes, coords)   # monocolor
  plt.tight_layout()
  plt.savefig(dist_dir+"/"+district+'.png',dpi=1000)

  return 
        
 p = multiprocessing.Pool(processes=multiprocessing.cpu_count()-1)
 
 for i in p.imap_unordered(doVoronoiForDistrict, range(len(districts))):
     print(i)

The procedure is relatively simple, but  the tessellation is computationally intensive, and would not be feasible on a personal computer at this scale. I threaded the tessellation for each district and ran the computation on two nodes of Oxford's Advanced Research Computing (ARC) high-throughput cluster, and it still took over 19 hours. However, I did it so you don't have to! Shapefiles for all districts in Punjab, Pakistan, can be downloaded here.

Comments

  1. AnonymousJune 27, 2021 at 3:37 AM

    Hi Ollies,

    This is really great work! Thank you!

    Do you know if anyone has developed the village shapefiles for KPK Province?

    ReplyDelete

Post a Comment

Popular posts from this blog

Calculating High-Resolution Standardized Precipitation-Evapotranspiration Index

-
Image
This post outlines a workflow for the calculation of a high-resolution version of the Stardardized Precipitation-Evapotranspiration Index (SPEI). This is accomplished in four steps, utilizing Python, R, and JavaScript. Quantifying the precise onset, duration, and end of droughts is difficult. Most approaches have historically measured drought as a prolonged deviation from the mean rainfall in an area. The Standardized Precipitation-Evapotranspiration Index (SPEI) builds on previous approaches by incorporating temperature data to account for the amount of water lost to evaporation. This is important because in an arid climate, a six week shortage in rainfall during the summer would have a much greater impact on soil moisture than the same shortage during the winter. This is especially important for drought forecasting that accounts for anthropogenic climate change. Indices that do not incorporate temperature data will persistently underestimate drought incidence as global t
Read more

Did Saudi Arabia Know an Attack was Coming?

-
Image
On September 14th 2019, a combination of drone and missile attacks targeted Saudi Arabia’s oil infrastructure at the Abqaiq and Khurais Aramco facilities, cutting the country’s oil production by over 50% and leading to the largest spike in the price of oil ever recorded . The attack was particularly embarrassing for Riyadh because billions of dollars' worth of air-defense systems were thwarted by drones that may have cost as little as $15,000 . A year later, the expert consensus seems to be that the attack was successful because the Saudis were caught off guard, with the element of surprise giving the assailants a decisive edge.  An open source analysis of radar interference from Saudi Arabian air defenses suggests that the Kingdom might actually have been expecting an Iranian attack on its oil infrastructure: five days before the attack, a missile defense system pointed at Iran was switched on for the first time at one of the largest refineries in the country. This analysis also
Read more

U.S. Foreign Military Sales Tracker

-
Image
Type the name of a country into the search box to view U.S. arms sales between 2001-2015 What are Foreign Military Sales (FMS) ? FMS is the primary process through which the U.S. Government sells weapons to the governments of other countries. In conducting FMS, the Department of Defense (DoD) acts largely as a brok er between foreign governments and U.S. arms manufacturers. The defense ministries of foreign governments submit a Letter of Request (LoR), which the U.S. State Department reviews. If approved, a DoD agency called the Defense Security Cooperation Agency (DSCA) mediates negotiations between the applicant and the contractor, levying a commission on the sale to finance its own operations. As such, the FMS program is operated at no net cost to taxpayers, but is slightly more expensive than private arms sales(Ibid). Once a request is approved by the DoD and DoS, it is sent to Congress for final approval. If the sale is successful, U.S. military personnel
Read more